Matthew West
Home CV Publications Students Projects

Variational Integrators

Variational integrators are a class of integration methods for Lagrangian systems, where the integrator is derived by discretizing Hamilton's principle of critical action rather than the ODE or PDE. A summary of the basic theory is given in Marsden and West (2001). These methods are automatically symplectic, with the resulting good energy behavior, and symmetries of the discrete Lagrangian result in momenta conserved by the integrator.

The conservative nature of variational integrators can allow substantially more accurate simulations at lower cost for conservative or weakly dissipative problems. For example, consider the determination of the temperature (average kinetic energy) of an isolated molecule (see Lew, Marsden, Ortiz, and West (2004)). The following figure compares the rate of convergence in time of a first-order explicit variational integrator (VI1) to that of a fourth-order explicit Runge-Kutta method (RK4). Despite the fact that the variational integrator is four times cheaper, it also converges far more quickly. This advantage is enhanced by using a fourth-order variational method, but this is not plotted as it is almost indistinguishable from the exact answer.

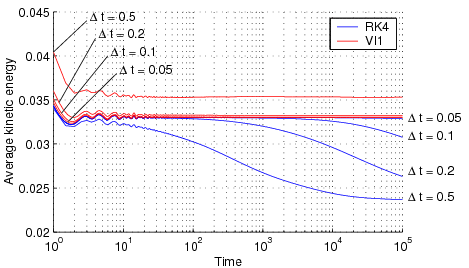While variational integrators are designed through a conservative Lagrangian mechanics framework, they are also highly applicable to near-conserative problems. For example, consider a weakly dissipative nonlinear oscillator (see Kane, Marsden, Ortiz, and West (2000)). The following figure shows the energy as a function of time for an exact benchmark solution, an explicit first-order variational integrator, and an explicit fourth-order Runge-Kutta method. The variational and Runge-Kutta integrators have the same step-size and so the variational method is four times cheaper. Despite this, it has far better long-time energy behavior (with some high-frequency oscillations). A fourth-order variational integrator at this step size is indistinguishable from the benchmark calculation.

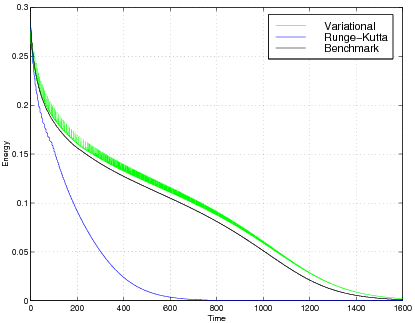As well as enabling the derivation of new methods, discrete variational mechanics serves as a powerful analysis tool for existing integrators. For example, it is easy to see that the Verlet method (the standard in molecular dynamics) is variational, and hence symplectic and conserving linear and angular momentum. Discrete variational mechanics provided the first proof that the conservative Newmark method is indeed symplectic in Kane, Marsden, Ortiz, and West (2000). This was not obvious due to the fact that Newmark preserves a non-canonical symplectic structure, and so the conservative nature of Newmark for nonlinear systems had been a mystery.

The idea of discrete mechanics is also very useful for deriving symplectic and conservative integrators for more challenging discretizations. Two examples of this are non-smooth sytems and asynchronous discretizations. In non-smooth mechanics a fully discrete formulation leads naturally to integrators for collision problems (see Fetecau, Marsden, Ortiz, and West (2003)). In asynchronous integrators, discrete variational mechanics provides a way to derive conservative symplectic integrators for PDEs where the solution advances non-uniformly in time, leading to AVIs (Asynchronous Variational Integrators).

Related publications